How to Think About Science

This article is a chapter from my newest book, Fitness Science Explained, which is live now in our store.

If you want a crash course in reading, understanding, and applying scientific research to optimize your health, fitness, and lifestyle, this book is for you.

Also, to celebrate this joyous occasion, I’m giving away $1,500 in Legion gift cards! Click here to learn how to win.

***

“Nothing has such power to broaden the mind as the ability to investigate systematically and truly all that comes under thy observation in life.”

—MARCUS AURELIUS

One of the biggest steps you can take toward both protecting yourself from bad science and benefitting from good science is learning how the scientific method works.

You know what it is in a general sense—the pursuit of knowledge, but you probably aren’t familiar with the exact steps that have to be taken to get that knowledge.

Once you understand the primary components of the scientific method, you can appraise “science-backed” claims for yourself and come to your own conclusions.

Let’s start at the top.

What Is Science?

Science is simply a way to think about a problem or set of observations.

We observe something in the world.

Then we think, “Hmmm, that’s interesting. I wonder why that happens.”

Next, we come up with ideas as to why it happens and then test them.

If our ideas fail the tests, then we test new ideas until something passes, at which point we can confidently say that the passing ideas may explain our original observations.

Basically, the scientific process goes like this:

We have a problem or set of observations that needs an explanation.
We formulate a hypothesis, a proposed explanation for our problem or set of observations.
We test the hypothesis using data.
If the data doesn’t support our hypothesis, then we change our hypothesis and test the new one.
If the data supports our hypothesis, we continue to test it using a variety of observations, more data collection, and multiple experiments.
If a set of related hypotheses is consistently and repeatedly upheld over a variety of observations and experiments, we call it a theory.

Much of science revolves around step #3, the process of hypothesis testing.

Scientific studies are the primary ways in which scientists engage in hypothesis testing, which, contrary to popular belief, doesn’t aim to prove whether something is “true,” but simply “most likely to be true.”

You can rarely prove something to be absolutely and universally true, but you can engage in a process of narrowing down what is most likely true by showing what isn’t true, and that’s science’s primary goal.

Hypothesis testing may sound abstract, but you actually do it every day.

Imagine a situation where your TV isn’t working.

This is step #1 in the above process; you have a problem (you can’t watch Game of Thrones).

You then formulate a hypothesis as to why the TV isn’t working (step #2). In this case, you hypothesize that it might be because it’s not plugged in.

You then engage in step #3 and test your hypothesis with data. In this case, you check behind the TV to see if it’s plugged in. If it isn’t plugged in, this can be considered support for your hypothesis.

To further test the hypothesis, you plug the TV in and try to turn it on. If it turns on, then you have arrived at the proper conclusion as to why the TV wasn’t working.

If the TV still doesn’t turn on even if it’s plugged in, however, then you’ve ruled out the plug as the problem. In essence, you’ve falsified your hypothesis that the problem was due to the plug.

You now have to change your hypothesis (step #4) to explain why the TV isn’t working.

Now you think that maybe it’s because the batteries in the remote are dead. This is your new hypothesis, and to test it, you press buttons on the remote and observe that the light on the remote doesn’t illuminate when you click the buttons. This supports your hypothesis, so you go grab new batteries to put in the remote.

In this way, you continue to go through steps 2 to 4, learning what isn’t true, until you narrow down the correct reason as to why your TV isn’t working.

When testing hypotheses, falsification is more important than support because, as mentioned above, you rarely can prove something to be unequivocally true. Rather, you arrive at the most likely explanation by showing what isn’t true.

Here’s an example to show you what this looks like in action.

Let’s say a professor has a classroom full of students, and he takes them through an exercise. He passes out a paper to all of the students that looks like this:

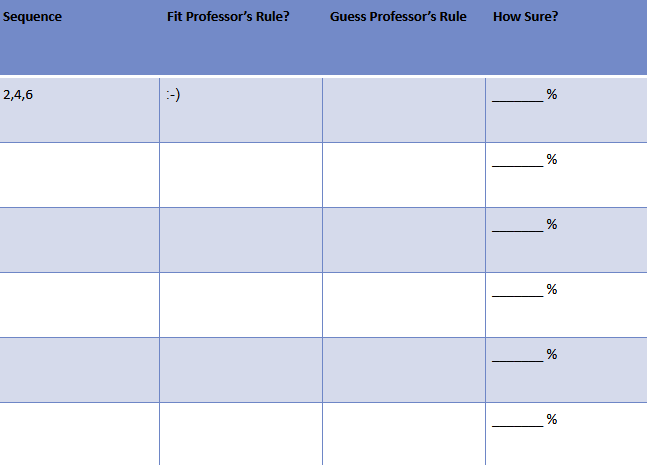
The professor tells all of his students that he has a rule in his head that can be used to generate number sequences. He gives the first sequence that fits with this rule—the sequence 2,4,6—and puts a smiley face next to it to signify this.

The professor then asks his students to guess the rule and write it on their sheets as well as estimate on a scale of 0-100 percent how certain they are that they’re correct. A typical student’s sheet might look like this:

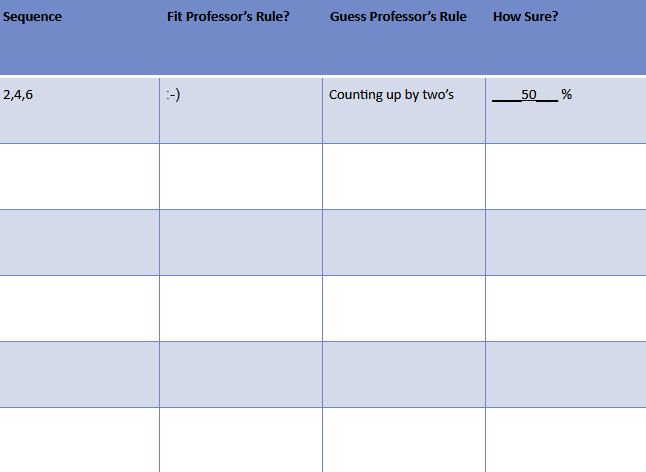
In this case, the student thinks that the rule is “counting up by two’s,” and she’s 50 percent sure this is correct.

The professor then asks his students to generate a new number sequence that they think might fit the rule. After they’ve done this, the professor draws smiley faces next to the sequences that fit and frowny faces for those that don’t. A typical student’s sheet may now look like this:

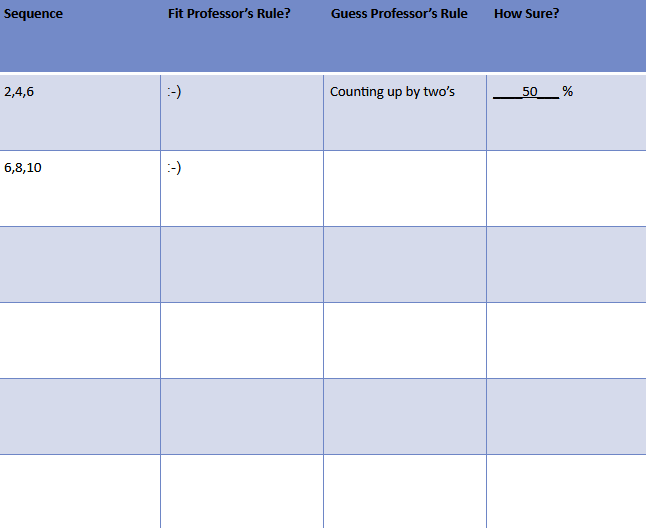
In this case, the student wrote “6, 8, 10” as a number sequence, and the professor indicated that it fit the rule.

Again, the professor asks the students to guess the rule, and write how certain they are that they’re correct. Now, a typical sheet might look like this.

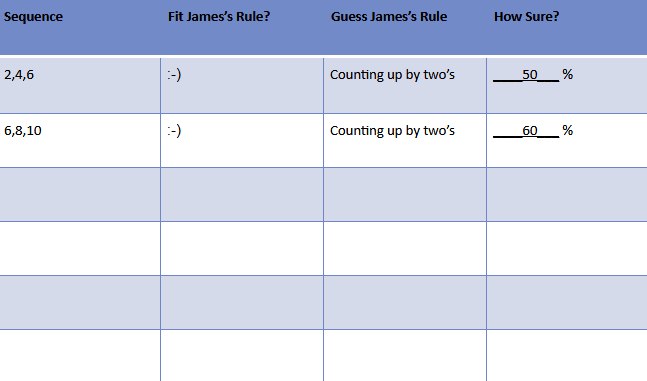
After doing this a number of times, a student’s sheet may look something like this:

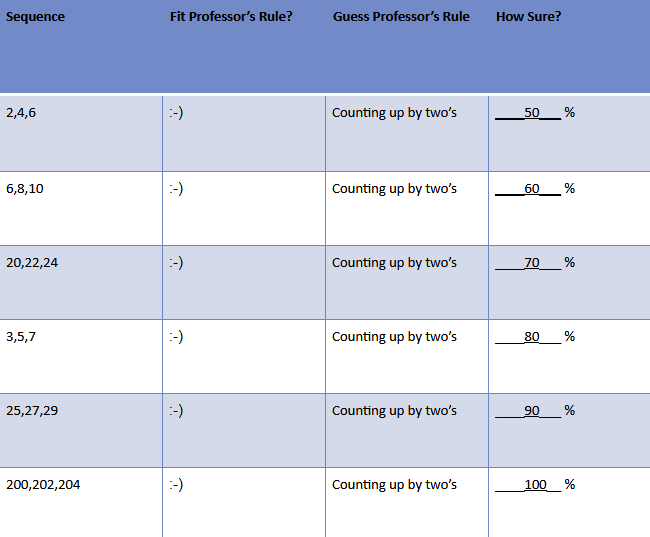
In this instance, the student has tested her hypothesis multiple times and is now 100 percent certain that the rule is “counting up by two’s.”

What about you? Do you agree?

Well, it turns out that the student is wrong—this is not the correct rule—and she would’ve realized this if she had tried to falsify the “counting up by two’s” hypothesis.

Instead, however, she continued to use number sequences that simply confirmed her belief that the rule was “counting up by two’s,” which led to a faulty conclusion.

Let’s look at how this student could test another number sequence to try to disprove her “counting up by two’s” hypothesis:

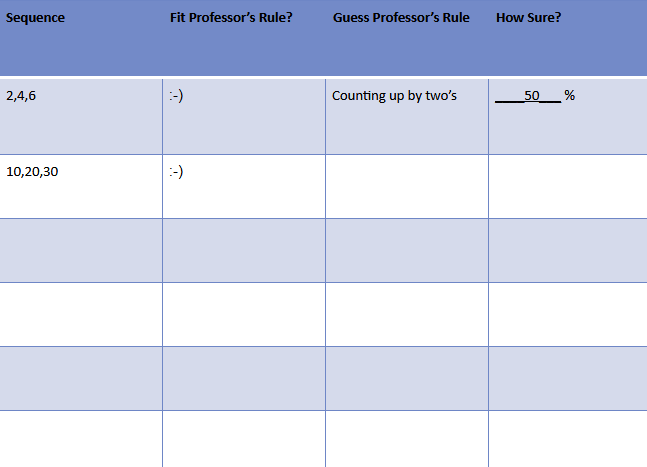
In this instance, the student wrote a number sequence that was NOT “counting up by two’s,” and received a smiley face.

So, the rule isn’t “counting up by two’s,” but perhaps some other variation of counting up. It’s time to test a new hypothesis, and she devises “counting up by multiples.”

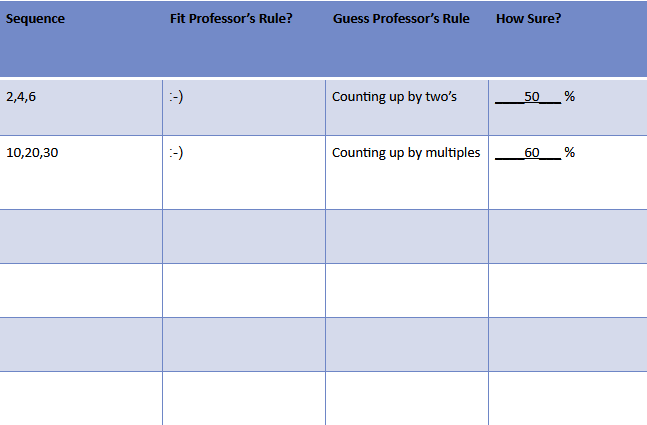
To test this new hypothesis (counting up by multiples), the student tries to disprove it by putting in a number sequence that is NOT counting up my multiples.

Once again, the professor indicates the sequence fits his rule, meaning the student is wrong again and must modify the hypothesis. Now, the student changes it to “counting up by even numbers.”

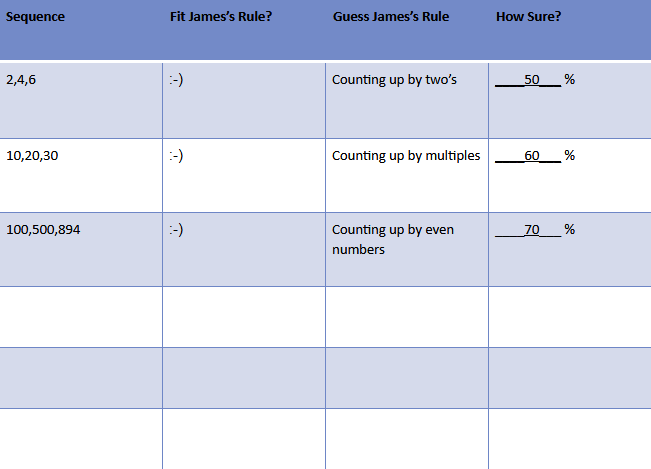
Correct again, but there’s still work to be done—namely, disproving this newest hypothesis of “counting up by even numbers.”

Eventually, through repeated testing and falsification, the student discovers the rule: “counting up.”

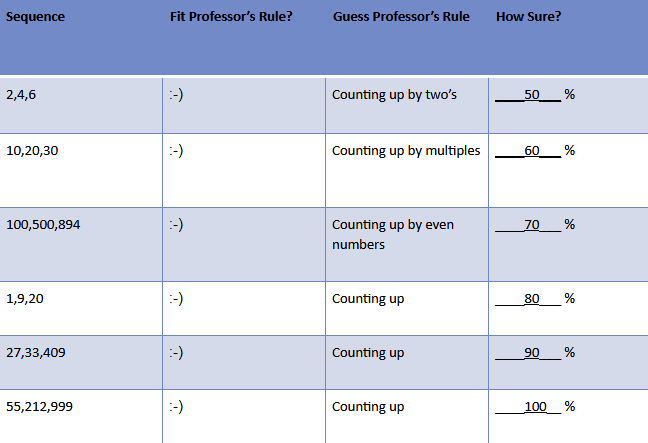
As you can see, falsification of hypotheses is a crucial part of discovering what’s true and what’s not, and that’s why it’s at the heart of how science works.

In real life, scenarios can be far more complicated, but the basic approach is the same.

Scientific research begins with a hypothesis and a set of predictions from that hypothesis, which are things that should be true, if our hypothesis is true.

These predictions are then tested by doing experiments and gathering data. If our predictions are shown to be false, then we need to modify our hypothesis or trash it for a new one.

If it pans out, then we know that our hypothesis may indeed be true, and if it continues to pan out in further research, we’ve created a valid theory.

So let’s say you had a hypothesis that Mike Matthews was Batman (hey, you never know!).

From this hypothesis, you would formulate a set of predictions that should be true if Mike and Batman were the same person. These predictions would include:

Mike and Batman won’t be in the exact same place at the exact same time.
Mike will consistently be missing when Batman appears, and vice versa.
Batman will most frequently turn up in areas of close proximity to where Mike lives.
Mike’s and Batman’s voices should have similarities.
Mike and Batman should be of similar height.
DNA testing should produce a match.

Failure of these predictions would indicate that Mike and Batman are not the same individual . . . but we may never be able to know for sure. 😉

Science works in this exact fashion.

We have a hypothesis (X is true). We then develop a set of predictions from that hypothesis (if X is true, then A, B, and C must be true). We then test our predictions with scientific studies. In other words, we do studies to see if A, B, and C are true. If they aren’t, then X is not true.

Here’s a real life example of hypothesis testing in the fitness world.

One popular hypothesis among some people is that carbohydrates make you fat, through the actions of the hormone insulin.

We know that eating carbs raises insulin levels, so when you eat a high-carb diet, your insulin levels are generally higher. We also know that insulin inhibits the breakdown of fat for energy and stimulates fat storage, so we can hypothesize that the high insulin levels produced by a high-carb diet will make fat loss more difficult.

The next step is developing a set of predictions from this hypothesis—things that should be true, if carbs and insulin actually make you fat. Some of these predictions could include:

Obese people should show less fat released from their fat tissue since they have higher insulin levels.
High insulin levels should predict future weight gain.
Fat loss should increase when we switch from a high-carb diet to a low-carb diet, while keeping protein and calorie intake the same.

There are many other predictions that could be developed from this hypothesis, but let’s just focus on these three, which have already been tested in experiments and shown to be false.

In one study, obese people show increased fat release from their fat tissue.
In another, high insulin levels did not predict future weight gain.
In yet another, fat loss was the same, or slightly less, when people switched to a low-carb diet compared to a high-carb diet with similar protein and calorie intake.

Given the failure of these predictions, we can confidently say that the hypothesis that “carbs make you fat via insulin” is false.

As scientists repeatedly develop hypotheses and test their predictions using research, the hypotheses that aren’t true get thrown out, and the hypotheses that are most likely to be true are kept.

Rather, the evidence to support a hypothesis accumulates over time, and the more high-quality evidence that exists to support it, the more true the hypothesis becomes.

As mentioned earlier, when a hypothesis or set of hypotheses is supported by a large body of high quality evidence that has withstood rigorous scrutiny through repeated testing, we call it a theory.

Given that science is based on the accumulation of evidence, its conclusions are always tentative. In other words, there is no such thing as 100% certainty in science (which is why you can’t absolutely prove anything).

Instead, there’s a degree of certainty, and that degree is based on how much evidence there is to support a scientific concept.

Some conclusions in science may be regarded with a high level of certainty due to the vast amount of supporting data and evidence, and others may be highly uncertain due to the lack of high-quality evidence.

You can imagine scientific research as a form of betting. In some areas of science, the data and conclusions are so strong that you would be willing to bet your life savings on it. In other areas, the data is so lacking that perhaps you might only be willing to bet $100 on it, or not even that.

The importance of accumulated evidence is why reproducibility is so important.

For a hypothesis to be true, the experiments that support it should be reproducible by scientists other than those who created it by repeating their experiments and observing the same results. This is also why considering the weight of the evidence is critical when coming to conclusions, and why science tends to move slowly over time.

An example of how conclusions rest on the strength of the evidence is the relationship between blood lipids and heart disease.

While some “pop-science” book authors have tried to question the relationship between blood levels of Low-Density Lipoproteins (LDL) and heart disease, the fact is that this relationship is very strong and is supported among multiple lines of evidence, and the evidence is also very strong that decreasing your LDL levels decreases your risk of atherosclerosis.

Thus, the evidence is overwhelming that elevated LDL causes heart disease; it’s the type of evidence you’d be willing to bet your life savings on.

Now, it’s also been suggested that High-Density Lipoproteins (HDL) are protective against heart disease. However, the evidence for that isn’t as strong; while observational studies support a relationship, studies that directly change your HDL via drugs haven’t shown any reduction in heart disease risk.

Thus, this is the type of evidence that perhaps you might only be willing to risk $100 on.

The Limitations of Science

While science represents our best tool for understanding and explaining the world around us, it isn’t without its limitations.

This is particularly true when it comes to exercise and nutrition research, whose limitations include, but aren’t limited to:

External Validity

External validity refers to the ability to extrapolate the results of a study to other situations and other people.

For example, equations used to estimate body composition in Caucasians don’t apply to African-Americans or Hispanics because the density of fat-free mass is different between different ethnicities.

There are many factors that can limit the external validity of a study. Some research is performed under highly controlled, artificial conditions, some is only performed on certain populations, like individuals with diabetes or other health conditions, and some studies may use protocols that don’t reflect what people do in real life.

Sample Size

Many studies in the field of exercise and nutrition have a very small number of subjects (often only 10 to 20 people per group).

This can make it difficult to extrapolate findings to thousands of people because small samples can increase the risk of random findings.

For example, as mentioned earlier, small studies suggested that antioxidant supplementation could reduce cancer risk. However, once larger studies came out, it was clear that antioxidant supplementation didn’t reduce cancer risk.

Small sample sizes can also make it more difficult to detect small but meaningful changes in certain variables. For example, some studies haven’t shown any differences in muscle size between low- and high-volume weight training.

However, these studies had a small number of subjects, and short-term changes in muscle size can be so small that they’re hard to detect. This may explain why an in-depth analysis of a number of studies on the topic has suggested that training volume does indeed impact muscle size.

Animal vs. Human Research

Animal studies have an advantage over human studies in that scientists have more control over the environment, activity, and food. This allows scientists to do a better job of isolating the variables they’re studying.

However, these studies can be limited in how much you can extrapolate the results to people, because animal physiology, while similar to humans, isn’t the same.

For example, rodents have a much greater capacity to convert carbs to fat, which means that high- versus low-carb studies in rodents aren’t necessarily applicable to people.

Lack of Control in Free-Living People and Inaccuracy of Self-Reporting

Many studies in the realms of exercise and nutrition are done on free-living individuals, that is, people living outside the controlled environment of a laboratory.

These studies are easier to conduct, but they’re also challenging because scientists are limited in how much they can control for unknown variables that can change the results.

For example, it’s been shown that people are notoriously inaccurate when reporting how food much they eat and how physically active they are, and therefore, studies that rely on self-reported food intake or physical activity may not be reliable.

Science is a systematic process for describing the world around us. Through the process of hypothesis testing and confirmation or falsification, we can eliminate what definitely isn’t true, and hone in on what’s most likely to be true.

The beauty of science is that it’s self-correcting, and is built on a body of evidence that’s accumulated and interpreted over time.

It has plenty of limitations, as do individual studies, but that doesn’t mean the scientific method or scientific experiments are fundamentally invalid. It just means we have to carefully consider the quantity and quality of evidence on a given matter when determining our level of certainty in our conclusions.

***

This article is a chapter from my newest book, Fitness Science Explained, which is live now in our store.

If you want a crash course in reading, understanding, and applying scientific research to optimize your health, fitness, and lifestyle, this book is for you.

Also, to celebrate this joyous occasion, I’m giving away $1,500 in Legion gift cards! Click here to learn how to win.

What Is Science?